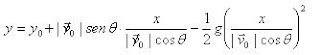Looping

 

 

Para que um corpo consiga dar a volta completa num looping, é necessário que apresente um valor mínimo de velocidade.

A seguir é apresentado um esquema das forças a considerar num looping em três situações distintas: no topo, na base e numa posição genérica.

Considerando desprezável o atrito e a resistência do ar, pode-se aplicar a Lei da Conservação da Energia para calcular a velocidade mínima que um corpo deve apresentar, em cada uma destas posições, para conseguir dar a volta ao looping.

 

No topo

No topo, a reacção normal tem o mesmo sentido que o peso. A força resultante só vai ter componente normal, pelo que:

E como as forças existentes são o peso e a reacção normal obtêm-se:

Mas como neste ponto Rn=0 a velocidade mínima vai ser:

 

Assim a velocidade mínima para não se cair no topo é de

Na base

Na base também existe uma velocidade mínima para que o carrinho faça o looping. Esta velocidade também pode ser calculada através da Lei da Conservação da Energia.

 

Assim se pode concluir que quanto maior for o raio do percurso, maior terá que ser a velocidade mínima para que o carrinho faça o looping.

No entanto, existem várias condições para que um carrinho ou simplesmente um outro objecto faça o looping.

Nas situações seguintes podemos verificar as diferentes condições:

 



 

Na situação 1 podemos verificar que o objecto descreve totalmente a trajectória circular do looping, uma vez que o raio que apresenta é menor que o raio da segunda situação.

 

Na situação 2, o objecto não finaliza a sua trajectória devido ao raio elevado da pista e por isso este cai.

 

Em ambas as situações a única variável é o raio da pista.

 

 

 

Nas seguintes situações podemos observar a variação de outros aspectos sem ser o raio, tais como a altura da pista e o local onde é abandonado o objecto.

Para finalizar, vamos demonstrar tudo isto que foi referido anteriormente com o vídeo seguinte:

 

 

Trabalho realizado por:

Paula Rocha n:16 12ºA

Renata Pinto n:22 12ºA

Tiago Branco n:24 12ºA

João Pardinhas n:25 12ºA

 

Pêndulo

Pêndulo de Newton

O Pêndulo de Newton

O pêndulo de Newton é um dispositivo que recebe o nome do físico Sir Isaac Newton por demonstrar empiricamente a conservação do momentum e da energia, leis físicas estudadas e demonstradas por Newton.

É construído a partir de uma série de pêndulos (normalmente 5) adjacentes uns aos outros. Cada pêndulo está anexado a uma armação por duas cordas de igual comprimento e ângulos opostos formados entre estas. Se essas cordas não fossem iguais em comprimento, as bolas ficariam desequilibradas. Esse arranjo de cordas restringe os movimentos do pêndulo ao mesmo plano.

É possível demonstrar de maneira simples o funcionamento do pêndulo de Newton. Sejam: m - massa que inicia a colisão (corresponde a massa de uma ou mais bolas); m2 - massa que parte após a colisão da massa m; v - velocidade da massa m antes da colisão; v1 - velocidade da massa m após a colisão; v2 - velocidade da massa m2 após a colisão.

Considerando que todas as bolas têm a mesma massa, m2 = x.m, onde x é o número de bolas que partem do outro lado do pêndulo de Newton.

Pelo princípio de conservação da quantidade de movimento:

mv = mv1 + m2v2 ® mv =

mv1 + (xm)v2 ® v = v1 + xv2     (1)

Considerando as colisões elásticas (coeficiente de restituição e = 1)

 (2)

Fazendo um sistema com as equações (1) e (2):

  (3)

Substituindo o resultado da equação do sistema na equação (2)

(4)

Pelo princípio de conservação da energia:

(5)

Substituindo a equação (3) na equação (4):

(6)

Igualando as equações (4) e (6):

O resultado comprova que o número de bolas que colidem numa extremidade é igual ao número de bolas que partem do outro lado.

Aqui fica o vídeo do seu funcionamento:

Trabalho realizado por: 

Bruno Sousa

Flávia Silva 

José Teixeira

Luís Coelho

Rúben Baião

12ºB  

Pêndulo Simples

      No dia-a-dia observamos vários tipos movimentos, e para os entender melhor vamos explorar o pêndulo simples que é o mais usado e permite o estudo dos movimentos oscilatórios e também da força do peso. 
     Existem vários tipos de pêndulos, como: os pêndulos físicos, de torção, cônicos, de Foucalt, duplos, espirais, de Karter e invertidos, mas o que vamos falar é o mais simples de todos.

  Retirado do sítio do Museu da Física da Escola Secundária Alexandre Herculano 

     Um pêndulo simples consiste num objeto, em que um corpo de massa m se encontra suspenso por um fio inextensível de comprimento l. 
     Quando o corpo se encontra na posição vertical, este encontra-se em repouso, isto é, na sua posição de equilíbrio, sendo apenas lhe aplicada a força gravítica ou peso e a tensão que o fio faz sobre o corpo. Mas quando este se encontra em movimento, tanto a direção, como a intensidade das forças aplicadas vão variando. 

     A força resultante segundo a direção do movimento é descrita pela seguinte equação:

 Fr = Px (=) Fr = m x g x sinα

     A força resultante segundo a componente vertical ao movimento é descrita pela seguinte equação: 

Fr = T - Py (=) Fr = T - m x g x cosα 

     Como nós sabemos que Fr = axm, e que como o corpo na posição de repouso contém apenas aceleração centrípeta, então para descobrirmos o valor de T, a equação irá ficar do seguinte modo: 

T = m x g x cosα + m x v/l 2 

     Na posição de equilíbrio a velocidade do pêndulo é máxima, assim como a tensão do fio.      
     Quando o corpo se encontra na sua posição extrema, ângulo máximo, atuam nele a tensão do fio, que se torna mínima, o peso do corpo e a força resultante tangente à trajetória, pois a força resultante é decomposta num sistema de eixos ligados ao pêndulo, mas neste caso, a força resultante normal é nula. 
     Através da posição extrema do corpo, iremos obter o valor da tensão do fio e também a aceleração tangencial. 
     Como sabemos a Fr=a x m, mas como a aceleração normal é nula , desse modo , a força resultante normal também será nula. 
     Então para chegar ao valor do T, recorremos à seguinte expressão:

 T= m x g x cosαmax 

     Como a força resultante tangencial é igual ao peso tangencial, poderemos encontrar a aceleração tangencial através da seguinte equação: 

at = g x sinαmax 

     Neste movimento a aceleração tem duas componentes, a aceleração normal e a aceleração tangencial, na qual estas variam o seu valor ao longo do movimento. 

• A aceleração normal é aquela que se vai modificando conforme a velocidade isto é, a sua aceleração é nula quando o corpo atinge o ponto máximo pois a sua velocidade também é nula, mas a aceleração é máxima quando o corpo se encontra na posição perpendicular ao solo, pois a sua velocidade é máxima nesse mesmo ponto. 
• A aceleração tangencial é aquela que se vai modificando conforme o ângulo que o pêndulo faz com a horizontal, sendo assim, a aceleração tangencial é nula quando o ângulo formado é mínimo e o valor da aceleração tangencial é máximo quando o ângulo formado também é máximo. O pêndulo gravítico pode ser utilizado com vários fins, desde de marcar os tempos a ilusões óticas. Fiquemos com um exemplo: 

Retirado de NatSciDemos Youtube

REALIZADO POR: 

Ana Moreira

Daniela Pinto

Emília Silva

Liliana Santos

12ºA 

Ano lectivo 2012/2013 

Forças de Atrito

Introdução

             Atrito, em física é a componente horizontal da força de contacto que actua sempre que dois corpos entram em choque e há tendência ao movimento. É gerada pela aspereza dos corpos. A força de atrito é sempre paralela às superfícies em interacção e contrária ao movimento relativo entre eles.

             Apesar de sempre paralelo às superfícies de interacção, o atrito entre estas superfícies depende da reacção normal, a componente vertical da força de contacto. Quanto maior for a reacção normal maior será o atrito.

            A força de atrito não depende da área de contacto entre as superfícies, apenas da natureza destas superfícies e da força normal.

Coeficiente de Atrito

        Os Coeficientes de atrito estático e de atrito cinético dependem apenas da natureza dos materiais em contacto e do seu polimento.
        O Coeficiente de atrito estático é determinado quando as superfícies em contacto encontram-se em iminência de movimento, mas ainda não se moveram.
        O Coeficiente de atrito cinético está presente a partir do momento que as superfícies em contacto apresentam movimento.
        O Coeficiente de atrito cinético será sempre menor que o Coeficiente de atrito cinético.

Atrito dinâmico ou cinético

Chama-se de força de atrito dinâmico à força que surge entre as superfícies que apresentam movimento entre si. A força de atrito dinâmico opõe-se sempre ao movimento, de forma a contrariá-lo e de certa forma impedi-lo.

A força de atrito cinético pode ser calculada pela seguinte expressão:

 ,medida em Newtons, e é o coeficiente de atrito cinético vezes  a reacção normal.

Quanto maior for a força normal, maior será o atrito entre os corpos.

Em relação à força de atrito estático a força que se opõe ao inicio do movimento entre superfícies

·           

E a força de atrito estático máximo relaciona-se com a reacção normal da seguinte forma:

·           (

Trabalho Prático

        Neste trabalho nós irmos mostrar que a força de atrito entre as folhas de duas listas telefónicas é tão grande que é impossível separar as listas.

Atrito entre duas folhas:3N

Atrito de uma folha entre duas outras é, aproximadamente, 6N pois a folha está a tentar mover-se em relação a duas superfícies (outras duas folhas).

Ora, se cada lista tem 1337 folhas e cada uma está sobre a acção de 6N de força de atrito que impede a separação, então 13379x6=8022N será a força necessária para separar as listas.

Mesmo dois tanques de guerra não conseguiriam separar as listas pois antes de se separarem elas rasgariam.

Demonstração do processo experimental:

Neste video é possível compreender melhor a força necessária para separar as duas listas telefónicas:

Mith Busters 

2006 / ep. 12

Discovery Channel

TRABALHO REALIZADO POR:

Ana Silva

Daniela Ferreira

Flávio Ferreira

Renata Sousa

Rui Cunha

12ºA 

Escola Secundaria Daniel Faria-Baltar

2012/13

Lançamento Horizontal e Oblíquo (Angry Birds e Top Gear)

Lançamento horizontal de um projétil

Existem os mais variados lançamentos horizontais de projéteis no dia-a-dia, a queda de um lápis que se encontra em movimento de uma mesa, a queda de um carro de uma ravina, etc.

Para descobrir as características deste movimento teremos de combinar as equações segundo xx e segundo yy.

Segundo xx obteremos uma equação onde a aceleração e a posição inicial serão zero. Consideramos na maior parte dos casos a posição inicial sendo 0. Mas é possível que esta não o seja em algumas situações. No caso da aceleração consideramos 0 porque durante o movimento, segundo xx, não existe nenhuma força a ser aplicada no projéctil. Logo segundo a direcção horizontal o movimento é uniforme.

Segundo yy obteremos uma equação em que não obteremos velocidade inicial, isto deve-se ao facto de que num lançamento horizontal o projétil adquire velocidade segundo o eixo do xx e não do yy. E obteremos aceleração provinda da força da gravidade, e a posição inicial será a altura de onde o projéctil foi lançado. Segundo o eixo dos yy o movimento será uniformemente acelerado já que segundo esta direcção actua a força da gravidade.

Os movimentos horizontais e verticais são independentes pois se deixarmos cair uma bola ( v_o=0) e lançarmos outra (v₀≠0) simultaneamente elas:

- Chegam ao solo simultaneamente;

- Encontram-se à mesma altura nos mesmos instantes de tempo;

Ao juntarmos a equação do movimento horizontal com a do movimento vertical obteremos uma equação do tipo:

Alcance num Lançamento Oblíquo

 No jogo que usamos para a apresentação (Angry Birds), o objetivo é determinar a distância da origem ao alvo para acertar no mesmo até ganhar o jogo.

Iremos mostrar como é que a partir das fórmulas de expressão normais, podemos chegar à fórmula direta para descobrir o alcance do projétil:

O ângulo formado entre o projétil e o a superfície chamaremos de θ, então:

Substituindo estas expressões da velocidade nas expressões de movimento:

Obteremos as expressões:

Isolando o tempo na expressão do xx e substituindo-a na expressão dos yy: 

Substituindo:

Como o alcance é máximo quando y=0:

(Nota: dado que estamos a considerar o x₀=0 e y₀=0, já anulei estas componentes)

Como:

Então, a expressão ficará com:

Isolando o x na expressão:

Substituindo de novo a tangente em sen θ e cos θ

Dado que:

Chegamos ao valor final da expressão:

Concluímos que o alcance máximo é quando o ângulo é de 45º porque:

sin (2x45º) =sin 90º e sin 90º=1

Trabalho realizado por:
José Fiuza 12ºA nº11
José Rocha 12ºA nº12
Miguel Silva 12ºA nº15
Raul Silva 12ºA nº20

Professora: Susana Fonseca

Física 12

2012/2013

O DILEMA DA FORÇA RESULTANTE

O DILEMA DA FORÇA RESULTANTE

Observe esta montagem e tente indicar em que sentido se vai deslocar cada um dos carros, inicialmente em repouso, quando se aumenta o peso de B ou o peso de A.

Ainda não chegou lá? Aqui estão pistas:

Independentemente do sistema estar em repouso ou não, todas as tensões se anulam 
(T₁= -T₂, T₃= -T₄, T₅= -T₆); no carro roxo, a componente do peso segundo y anula com a reação normal, e no carro azul, o peso também anula com a reação normal.

Quando o sistema está em repouso (Fr=0), pois P_A= P_B.

Se, mesmo assim, ainda não chegou lá ou se quer confirmar a sua teoria, aqui tem a resolução deste desafio:

A força resultante que atua no plano horizontal consiste na subtração entre o peso de B e o peso de A, P_B – P_A (pois são as únicas forças que não se anulam no sistema, logo, a resultante vai resultar da diferença entre elas)

A força resultante que atua no plano inclinado consiste na componente do peso segundo x, P_Cx (única força que, neste sistema, também não se anula).

Logo, a força resultante do sistema será P_Cx – (P_B – P_A).

Quando se aumenta o peso de A:

Quando o peso de A, P_A, aumenta, P_B – P_A < 0. Logo, o carrinho azul desloca-se segundo o sentido negativo da trajetória.

Assim, P_Cx – (P_B – P_A) > 0, pelo que o carrinho roxo irá movimentar-se segundo o sentido positivo da trajetória.

Portanto, quando se aumenta o peso de A, o carrinho azul desloca-se para o sentido esquerdo, o que fará com que o carrinho roxo suba a rampa.

Quando se aumenta o peso de B:

Quando o peso de B, P_B, aumenta, P_B – P_A > 0. Logo, o carrinho azul desloca-se segundo o sentido positivo da trajetória.

Assim, P_Cx – (P_B – P_A) < 0 (pois P_Cx < P_B – P_A), pelo que o carrinho roxo desloca-se no sentido negativo da trajetória.

Portanto, quando se aumenta o peso de B, o carrinho azul irá deslocar-se para o sentido direito, o que fará com que o carrinho roxo desça a rampa.

Não acredita? Veja por si mesmo:

Quanto à demonstração em que se verifica o aumento do peso de A, iremos deixar a questão no ar, de modo a que você mesmo comprove fazendo um sistema igual ao nosso! Boa sorte.

Realizado por:

• Catarina Ferreira 12ºB nº2
• Filipe Ferreira 12ºB nº9
• Pedro Barbosa 12ºB nº20
• Pedro Martins 12ºB nº21
• Ricardo Sousa 12ºB nº23

Professora:

• Susana Fonseca

Ano Letivo 2012/2013

Escola Secundária Daniel Faria – Baltar