Lançamento horizontal de um
projétil
Existem os mais variados
lançamentos horizontais de projéteis no dia-a-dia, a queda de um lápis que se
encontra em movimento de uma mesa, a queda de um carro de uma ravina, etc.
Para descobrir as características
deste movimento teremos de combinar as equações segundo xx e segundo yy.
Segundo xx obteremos uma equação onde a aceleração e a posição inicial
serão zero. Consideramos na maior parte dos casos a posição inicial sendo 0. Mas
é possível que esta não o seja em algumas situações. No caso da aceleração
consideramos 0 porque durante o movimento, segundo xx, não existe nenhuma força a ser aplicada no projéctil. Logo
segundo a direcção horizontal o movimento é uniforme.
Segundo yy obteremos uma equação em que não obteremos velocidade inicial,
isto deve-se ao facto de que num lançamento horizontal o projétil adquire
velocidade segundo o eixo do xx e não
do yy. E obteremos aceleração
provinda da força da gravidade, e a posição inicial será a altura de onde o projéctil
foi lançado. Segundo o eixo dos yy o movimento será uniformemente acelerado já
que segundo esta direcção actua a força da gravidade.
Os movimentos horizontais e
verticais são independentes pois se deixarmos cair uma bola ( vo=0)
e lançarmos outra (v0≠0) simultaneamente elas:
- Chegam ao solo simultaneamente;
- Encontram-se à mesma altura nos
mesmos instantes de tempo;
Ao juntarmos a equação do
movimento horizontal com a do movimento vertical obteremos uma equação do tipo:
Alcance num Lançamento
Oblíquo
No jogo que
usamos para a apresentação (Angry Birds), o objetivo é determinar a distância
da origem ao alvo para acertar no mesmo até ganhar o jogo.
Iremos mostrar como é que a partir das fórmulas de expressão normais, podemos
chegar à fórmula direta para descobrir o alcance do projétil:
O ângulo formado entre o projétil e o a superfície chamaremos de θ, então:
Substituindo
estas expressões da velocidade nas expressões de movimento:
Obteremos
as expressões:
Isolando
o tempo na expressão do xx e substituindo-a na expressão dos yy:
Substituindo:
Como o alcance é máximo
quando y=0:
(Nota: dado que estamos
a considerar o x0=0 e y0=0, já anulei estas
componentes)
Isolando o x na expressão:
Substituindo de novo a
tangente em sen θ
e cos θ
Dado que:
Chegamos ao valor final
da expressão:
Concluímos que o alcance
máximo é quando o ângulo é de 45º porque:
sin (2x45º) =sin 90º e sin 90º=1
Trabalho realizado por:
José Fiuza 12ºA nº11
José Rocha 12ºA nº12
Miguel Silva 12ºA nº15
Raul Silva 12ºA nº20
Professora: Susana Fonseca
Física 12
2012/2013








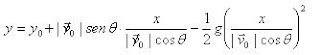








Sem comentários:
Enviar um comentário